Cisco Converting from Decimal to Binary

In this Cisco CCNA tutorial, I’m going to show you how to convert decimal to binary, which will help you understand IP addressing. Scroll down for the video and also the text tutorial.

Cisco Converting from Decimal to Binary Video Tutorial

 

IP addresses are written down in a decimal format. But to understand how they control the logical separation between networks, it really helps if you think about them the same way that a computer does, and that is in binary.

 

Counting in Decimal

 

As humans, we are conditioned to count in decimal. It's how we're taught to do it from a really young age, and we do it now without thinking about it.

 

 

When we write a number down, for each column in the number, we have got 10 possible choices from 0 through to 9, and every time we add a column to the left, the value is multiplied by 10.

 

We start with 1's as the furthest right column. When we write down a number, starting from the right-hand side of a number, we've got the 1's there.

 

The next column is the 10's, then we've got the 100's, then the 1000's, then the 10000's, and so on. You can see that it's being multiplied by 10 each time we add a column to the left.

 

 

If we were going to write down the number 236, the way that we do that is starting from the left now. Starting with the 1000s column, how many 1000s can we fit into 236?

 

Well, obviously, that's going to be a 0 because 236 is a smaller number than 1000. Since we can't fit any 1000s into 236, that leaves us still with 236 leftover.

 

Next up, how many 100s can we fit into 236? Well, we can fit two 100s into 236, and that leaves us with 36 leftover.

 

Next up, how many 10s can we fit into the 36 that was leftover? We can fit three 10s into 36, and that leaves us with 6 leftover.

 

Lastly, how many 1s can we fit into 6? That's obviously 6. So, that gives us the number 236. It's how we would write that down.

 

Decimal is completely obvious and intuitive, so you may be wondering why I'm breaking it down like that. Well, it's because binary is not obvious and intuitive, but it works the same way.

 

Counting in Binary

 

Seeing how it works with decimal is then going to help understand and see how it works with binary. Computers don't work in decimal. They work in binary, and electrical impulses are either off or on.

 

There are only 2 choices, a 0 or a 1, unlike the 10 choices that we have in decimal, which are 0 through 9. Every time we write down a number in binary for each column in the number, we've got two possible choices, that's 0 or 1, rather than 0-9 that we had in decimal.

 

 

Every time we add a column to the left, the value is multiplied by 2, rather than multiplied by 10 as it is in decimal. So looking at the columns in binary now, again, we've got a 1 on the furthest right, the same as it was in decimal.

 

Then, we multiply that by 2, so the next is 2, then we've got 4, then we've got 8, so we just keep multiplying by 2, just doubling it each time. Next would be 16, then 32, then 64, then 128, then 256, then 512, and so on.

 

You saw how to write 236 in decimal before. Now, let's see how to write 236 in binary. You can see on the image below that the number we're going to get in the end is 11101100.

 

 

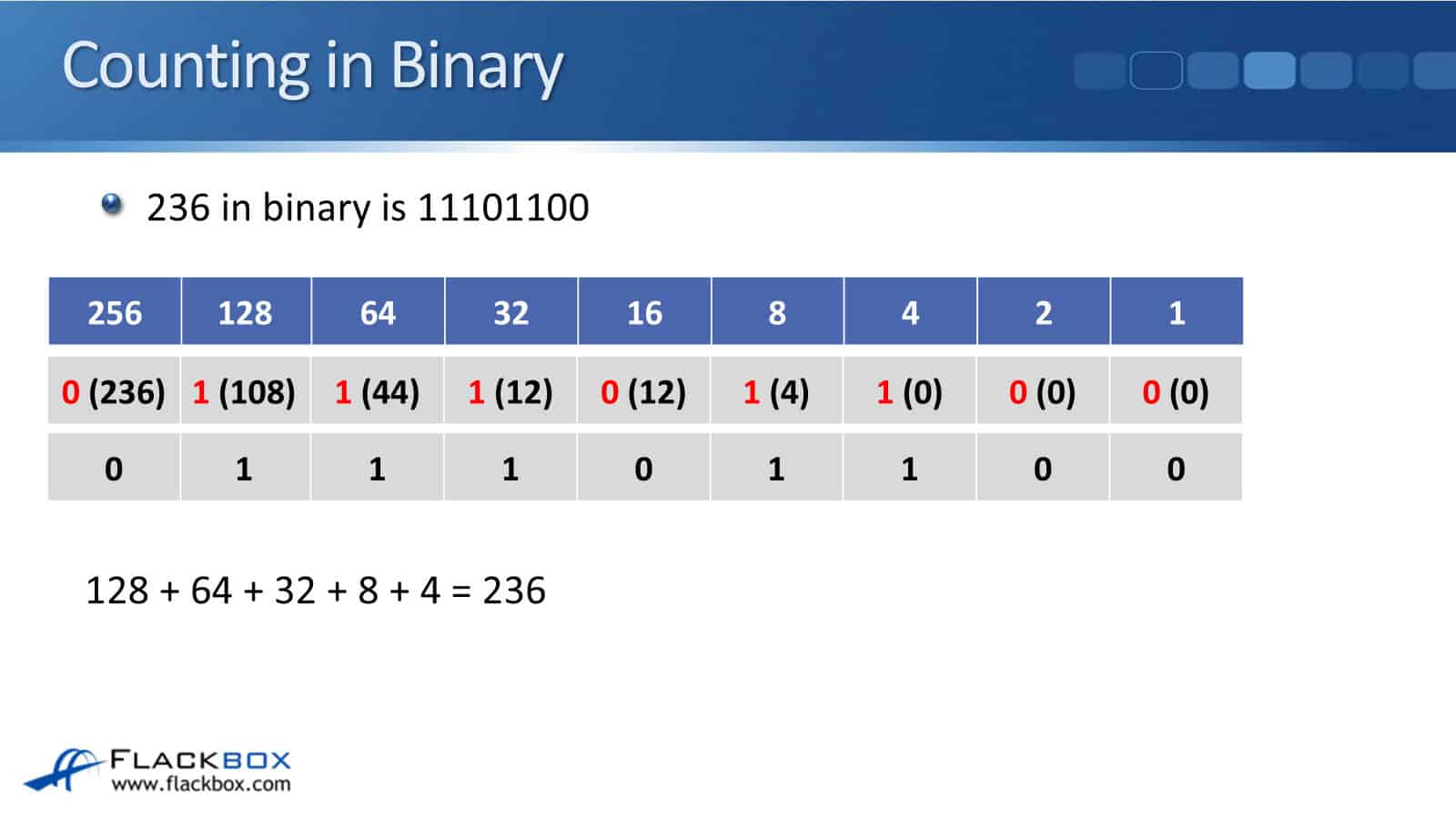
It's not really intuitive like it is with decimal, but we do it the same way. Rather than seeing how many we can fit in, it's either going to be on or off, 1 or 0.

 

So starting off with 256 here, does 256 fit into 236, yes or no? Well, no. It doesn't. 236 is a smaller number than 256, so we can fit zero 256s into 236, and that leaves us with 236 leftover.

 

Next up, can we fit 128 in 236 or not? The answer is yes. So that gives us a 1, and we've got 108 leftover because 236 minus 128 is 108.

 

So, next up, does 64 fit into that 108 that was leftover or not? Yes, it does, so we put down a 1, and we've got 44 leftover because 108 minus 64 is 44.

 

Next, does 32 fit into the 44 that was leftover? Yes, it does, so we have a 1 again, and we've got 12 leftover now. Then, does 16 fit into 12 or not? No, it doesn't, so we put a 0 down, and we've still got 12 leftover.

 

Then does 8 fit in 12 or not? Yes, it does, so that's a 1, and we've got 4 leftover. Then, does 4 fit into 4? Yes, it does, so we put a 1 down, and that leaves us with 0 leftover.

 

So obviously, the other two digits are going to be a 0 and a 0 because 2 and 1 do not fit into 0. You can see there that when we've got it written out, that comes out to 11101100. That is 236 in binary.

 

As a final check, you should always have 0 leftover, so if you get down to the 1 column and you've still got digits leftover there, that means that you've made a mistake, so you should go back and do it again.

 

You can also do a final check of your answer as well, where you do add up all of the columns where you've got a 1. Add them all together, and that should total up the number you were looking for.

 

In our example here, we've got a 1 in the 128, a 1 in the 64, a 1 in the 32, in the 8, and in the 4. If we add up 128 and 64 and 32, add 8, and add 4, that will be equal to 236, which was the number that we were looking to calculate.

 

Next example, what is 179 in binary? The easiest way to do it is to get a pen and piece of paper and write the columns down exactly like you see on the slide here, and then just go from left to right.

 

 

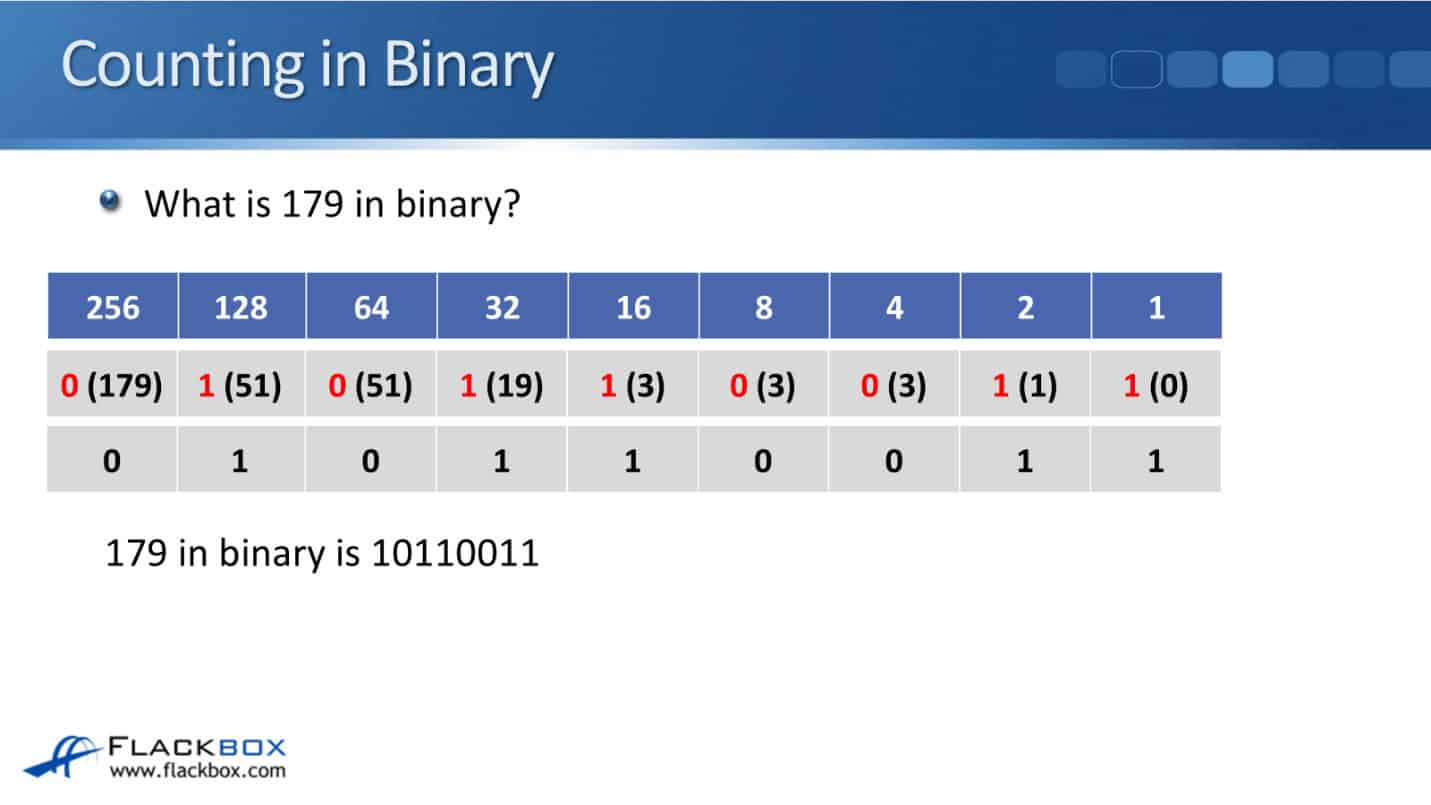
To figure out 179 in binary, let's start with, does 256 fit into 179, yes or no? No, it does not, so we put down a 0, and we've still got 179 left.

 

Then, does 128 fit into 179 or not? Yes, it does, so we put down a 1, and we've got 51 left. Next, does 64 fit into 51? No, it does not. So we put down a 0, and we've still got 51 leftover.

 

Then, does 32 fit into 51 or not? Yes, it does, and 51 minus 32 is 19, so we've got 19 leftover. Then, does 16 fit into 19 or not? Yes, it does. We put down the 1, and we've got 3 leftover.

 

Does 8 fit into 3? No, it doesn't, so we put down 0, and we've still got the 3 leftover. Does 4 fit into 3? No, it doesn't, so again, we put down 0, and we've still got 3 leftover.

 

Then, does 2 fit into 3? Yes, it does, so we put down a 1, and we've got a 1 leftover. And finally, 1 does go into 1, so we put a 1 there, and then we've got our 0 leftover. So, writing down 179 in binary is 10110011.

 

Additional Resources

 

Binary Game: https://learningnetwork.cisco.com/s/binary-game

Understanding Binary Basics: https://www.learncisco.net/courses/icnd-1/lan-connections/binary-basics.html

Converting the Decimal IP Address to Binary: https://study-ccna.com/converting-ip-address-decimal-to-binary/

 

Want to practice Cisco CCNA technologies on your laptop? Download my complete 350-page Cisco CCNA Lab Guide for free.

 

Click Here to get my Cisco CCNA Gold Bootcamp, the highest rated CCNA course online with a 4.8 star rating from over 20,000 public reviews.